Recursive Function Example
Recursive Function Example - Web Oct 4 2021 nbsp 0183 32 While the Ackermann function has some application in advanced mathematics it is mostly known for being an example of a highly recursive function Even slight increases to its two integer arguments cause a large increase in the number of recursive calls it makes Web In this module we ll see how to use recursion to compute the factorial function to determine whether a word is a palindrome to compute powers of a number to draw a type of fractal and to solve the ancient Towers of Hanoi problem Web As an example we show how recursion can be used to define and compute the factorial of an integer number The factorial of an integer n is 1 215 2 215 3 215 215 n 1 215 n The recursive definition can be written 1 f n 1 if n 1 n 215 f n 1 otherwise The base case is n 1 which is trivial to compute f 1 1
Look no even more than printable templates in case that you are looking for a effective and easy method to improve your productivity. These time-saving tools are free and easy to utilize, supplying a variety of advantages that can help you get more done in less time.
Recursive Function Example
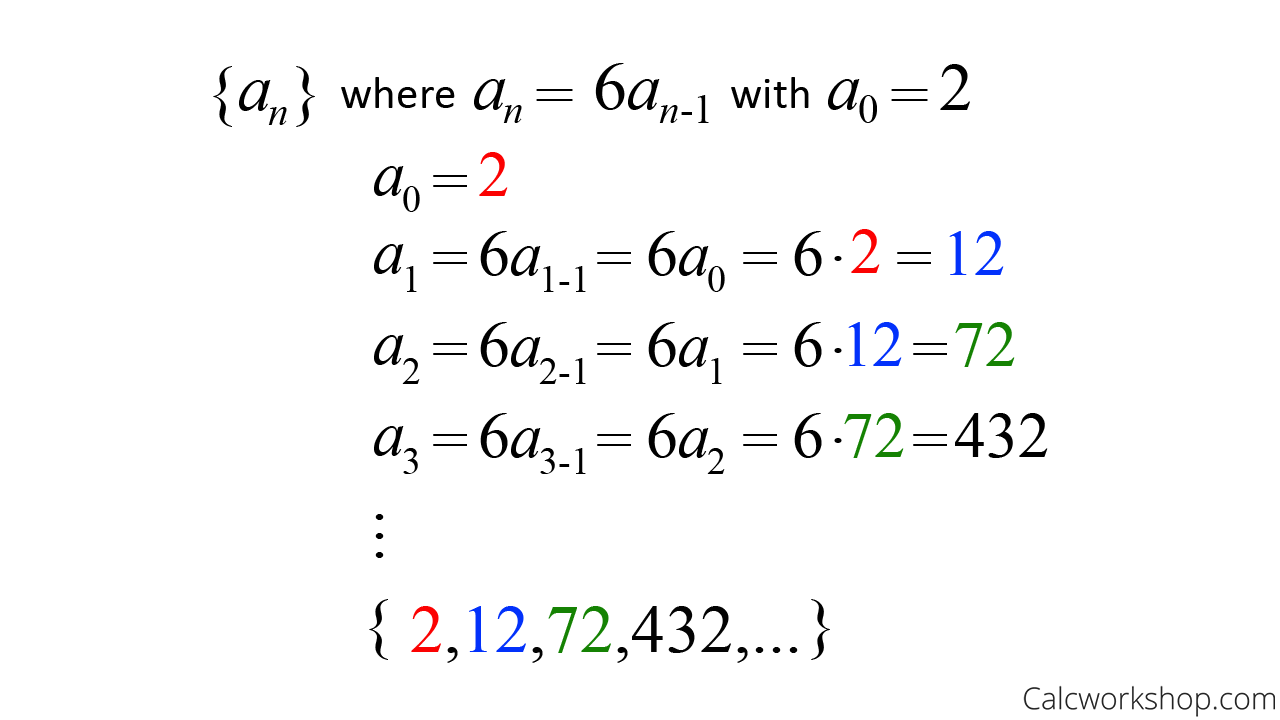
Example Of A Recursive Function In Math
 Example Of A Recursive Function In Math
Example Of A Recursive Function In Math
Recursive Function Example Firstly, printable templates can assist you remain organized. By offering a clear structure for your jobs, to-do lists, and schedules, printable templates make it simpler to keep everything in order. You'll never ever need to fret about missing out on deadlines or forgetting essential jobs again. Using printable templates can assist you save time. By eliminating the need to develop new documents from scratch whenever you require to finish a job or plan an occasion, you can focus on the work itself, instead of the documents. Plus, numerous templates are personalized, allowing you to personalize them to fit your needs. In addition to conserving time and staying arranged, utilizing printable templates can also help you remain encouraged. Seeing your progress on paper can be a powerful incentive, motivating you to keep working towards your goals even when things get difficult. In general, printable templates are a fantastic method to improve your efficiency without breaking the bank. Why not provide them a shot today and start attaining more in less time?
Find Fibonacci Sequence Number Using Recursion In JavaScript Nathan
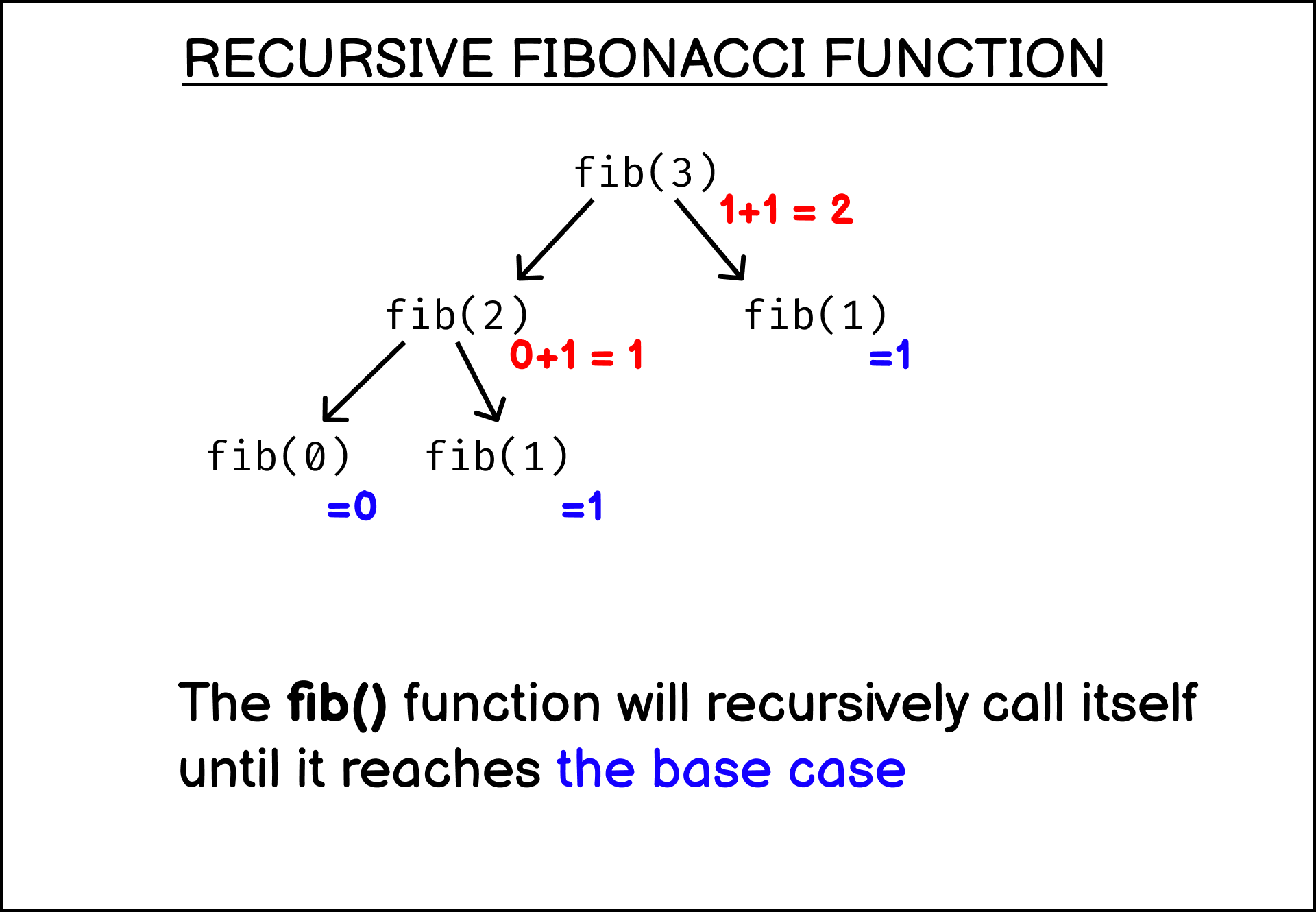 Find fibonacci sequence number using recursion in javascript nathan
Find fibonacci sequence number using recursion in javascript nathan
Web Example Sum of Natural Numbers Using Recursion include lt stdio h gt int sum int n int main int number result printf quot Enter a positive integer quot scanf quot d quot amp number result sum number printf quot sum d quot result return 0 int sum int n if n 0 sum function calls itself return n sum n 1 else return n Output
Web Sep 20 2008 nbsp 0183 32 1 I use recursion all the time but usually for mathy and graphy things I m trying to look for examples of recursion that would be meaningful to non programmers redfood
2 Things That I Am Confused About Tail Recursion Stack Overflow
 2 things that i am confused about tail recursion stack overflow
2 things that i am confused about tail recursion stack overflow
Recursive Function In C Syntax Execution Of Recursive Function In C
 Recursive function in c syntax execution of recursive function in c
Recursive function in c syntax execution of recursive function in c
Free printable design templates can be an effective tool for improving efficiency and accomplishing your objectives. By selecting the ideal templates, integrating them into your regimen, and customizing them as needed, you can enhance your everyday tasks and make the most of your time. So why not give it a try and see how it works for you?
Web Example of a recursive function def factorial x quot quot quot This is a recursive function to find the factorial of an integer quot quot quot if x 1 return 1 else return x factorial x 1 num 3 print quot The factorial of quot num quot is quot factorial num Run Code Output The factorial of 3 is 6
Web For example recursive computation of 4 looks like this Recursive Calculation of 4 The calculations of 4 3 and 2 suspend until the algorithm reaches the base case where n 1 At that point 1 is computable without further recursion and the