How To Find Standard Deviation
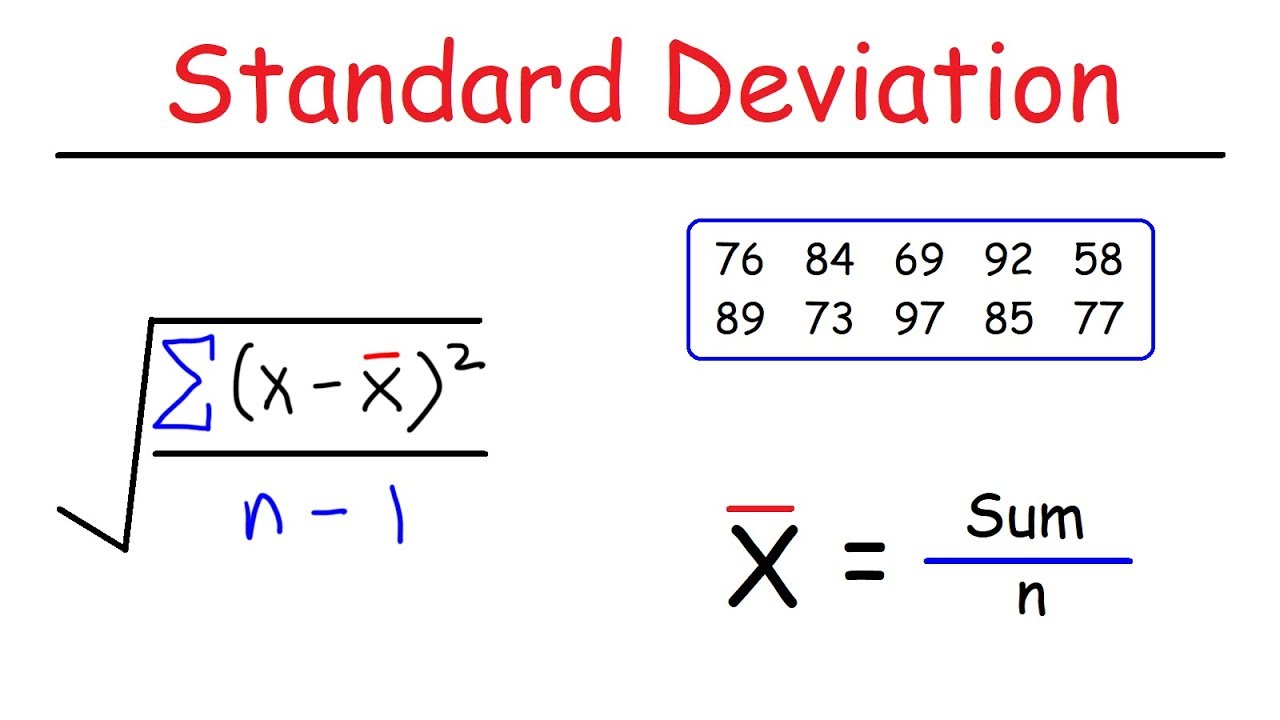
How To Find Standard Deviation - To calculate standard deviation start by calculating the mean or average of your data set Then subtract the mean from all of the numbers in your data set and square each of the differences Next add all the squared numbers together and divide the sum by n minus 1 where n equals how many numbers are in your data set You can calculate the standard deviation by hand or with the help of our standard deviation calculator below Steps for calculating the standard deviation by hand The standard deviation is usually calculated automatically by whichever software you use for your statistical analysis General Education Standard deviation is a way to calculate how spread out data is You can use the standard deviation formula to find the average of the averages of multiple sets of data Confused by what that means How do
Look no further than printable templates in case that you are looking for a easy and efficient method to increase your productivity. These time-saving tools are free-and-easy to utilize, providing a series of benefits that can assist you get more carried out in less time.
How To Find Standard Deviation
How To Calculate Standard Deviation From Mean And Sample Size Haiper
How To Calculate Standard Deviation From Mean And Sample Size Haiper
How To Find Standard Deviation Firstly, printable design templates can help you stay organized. By supplying a clear structure for your jobs, order of business, and schedules, printable design templates make it simpler to keep everything in order. You'll never need to stress over missing due dates or forgetting essential tasks once again. Secondly, using printable design templates can help you save time. By eliminating the need to create brand-new files from scratch whenever you require to finish a task or plan an occasion, you can concentrate on the work itself, rather than the documents. Plus, lots of design templates are personalized, enabling you to individualize them to suit your requirements. In addition to conserving time and remaining organized, utilizing printable design templates can likewise help you remain encouraged. Seeing your development on paper can be a powerful motivator, encouraging you to keep working towards your objectives even when things get difficult. Overall, printable templates are a great way to improve your productivity without breaking the bank. Why not offer them a try today and start accomplishing more in less time?
How To Calculate Standard Deviation Using Mean Haiper
How to calculate standard deviation using mean haiper
Standard deviation calculates the extent to which the values differ from the average Standard Deviation the most widely used measure of dispersion is based on all values Therefore a change in even one value affects the value of standard deviation It is independent of origin but not of scale
Step 1 Work out the mean In the formula above the greek letter mu is the mean of all our values Example 9 2 5 4 12 7 8 11 9 3 7 4 12 5 4 10 9 6 9 4 The mean is 9 2 5 4 12 7 8 11 9 3 7 4 12 5 4 10 9 6 9 4 20 140 20 7 And so 7 Step 2 Then for each number subtract the Mean and square the result
How To Calculate Median From Mean And Standard Deviation Haiper
/calculate-a-sample-standard-deviation-3126345-v4-CS-01-5b76f58f46e0fb0050bb4ab2.png "How To Calculate Median From Mean And Standard Deviation Haiper")
How to calculate median from mean and standard deviation haiper
What Is Standard Deviation Formula For Calculating Standard Deviation
What is standard deviation formula for calculating standard deviation
Free printable templates can be an effective tool for increasing performance and achieving your objectives. By choosing the ideal templates, integrating them into your regimen, and customizing them as needed, you can enhance your day-to-day tasks and maximize your time. Why not provide it a try and see how it works for you?
Generally calculating standard deviation is valuable any time it is desired to know how far from the mean a typical value from a distribution can be This free standard deviation calculator computes the standard deviation variance
The standard deviation SD is a single number that summarizes the variability in a dataset It represents the typical distance between each data point and the mean Smaller values indicate that the data points cluster closer to the mean the values in the dataset are relatively consistent